서로서 집합은 상호 배타적 집합(Disjoint-set) 이라고 한다.
교집합이 공집합인 집합(서로소 집합) 들의 정보를 확인하고 조작할 수 있는 자료구조이다.
- union : 두 노드를 한 그래프로 합친다.
- find : 어떤 노드가 속한 집합을 반환
이 문제는 유니온 파인드를 이용하여 두 노드가 해당하는 집합을 합치거나 한 노드가 다른 노드의 집합에 속하는지 판별하는 문제이다.
따라서 union함수를 구현하고, find함수를 구현하여 풀이를 진행한다.
우선 find함수를 구현한다. find함수의 역할은 해당 노드의 부모로 탐색을 진행한다. 따라서 루트 노드를 만나는 경우 반환을 진행하며, 루트 노드가 아닌 경우에는 해당 노드의 부모에 루트 노드 값을 입력해준다. (즉 find과정을 통해 tree를 재 갱신함으로써 한 그룹에 속해 있다는 것을 명시해줄 수 있다.)
즉 {1,6,7} 이라고 가정한다. 그럼 (노드, 부모) 라고 한다면 (1,1),(6,1),(7,6)을 가지게 되는데 이때 find함수를 통해 (1,1),(6,1),(7,1)로 바뀌게 된다. 이는 재귀를 통해 매번 부모 값을 재갱신 시키기 때문이다.


int find(int node){
if(tree[node] == node) return node; //자기 자신인경우
return tree[node] = find(tree[node]);
}
union함수의 역할은 두 노드의 루트 노드를 찾아온 뒤 a노드의 부모에 b노드의 루트 노드 값을 할당한다.
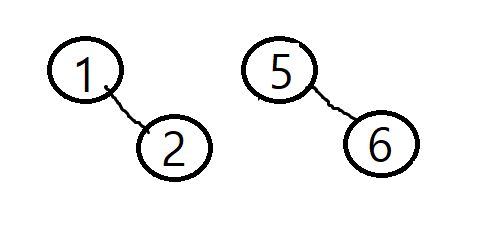
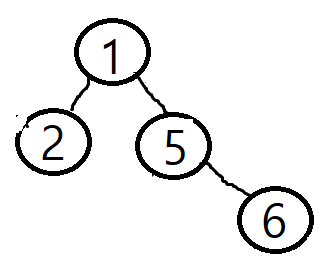
이를 통해 a노드는 b노드로 편입하게 된다. 만약 2와 6을 union한다고 하면 2의 루트 1과, 6의 루트 5를 구하게 된다.
그럼 tree[5] = 1을 대입하여 5의 부모노드가 1이 되고 그래프는 오른쪽과 같이 변경된다.
void union(int a, int b) {
int pa = find(a);
int pb = find(b);
tree[pa] = pb;
}
이제 유니온과 파인드가 어떤 역할을 하는지 알 수 있다. 즉 노드를 그룹핑하는데에 사용된다.
이제 이를 이용하여 그룹을 만들어보고 두 노드가 서로 같은 집합인지 아닌지 알아내는 코드를 짜보자.
#include<iostream>
using namespace std;
int M[1000001];
int Find(int c) {
if (M[c] == c) return c;
return M[c] = Find(M[c]); //여기서 각 그룹이 동기화?
}
void Union(int a, int b) {
int pa = Find(a);
int pb = Find(b);
M[pa] = pb;
}
int main() {
cin.tie(0);
cin.sync_with_stdio(false);
ios_base::sync_with_stdio(false);
int n, m;
cin >> n >> m;
for (int i = 1; i < n+1; i++)
{
M[i] = i; // 초기에는 서로 그룹핑됨.
}
for (int i = 0; i < m; i++)
{
int a, b, c;
cin >> a >> b >> c;
if (a == 0) {//union
Union(b, c);
}
else {//find검증
if (Find(b) == Find(c)) {
cout << "YES\n";
}
else {
cout << "NO\n";
}
}
}
}
이번 특강을 통해 너무 어려운게 많다. 그나마 유니온 파인드는 따라갈 만 했으나 꼬아서 나온다면 어느정도로 나올지 모르겠다. 더 열심히 하자.
결론은 유니온 파인드는 합집합 연산에 사용한다는것.
'알고리즘' 카테고리의 다른 글
| [c++] 백준 1753 풀이 ( 최단 경로, 다익스트라, 그래프, 우선순위 ) (0) | 2021.08.04 |
|---|---|
| [c++] 백준 1197 풀이 (MST, 최소 신장 트리, 그래프, 유니온 파인드) (0) | 2021.08.02 |
| [python3] 백준 1967 풀이 (트리의 지름, DFS) (0) | 2021.07.26 |
| [python3] 백준 1937 풀이 (욕심쟁이 판다, DFS, DP) (0) | 2021.07.26 |
| [py3] 백준 2573 풀이 (빙산, DFS, 그래프) (0) | 2021.07.24 |
![[c++] 백준 1717 풀이 (집합의 표현, 그래프, 서로소 집합, 유니온파인드)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fc0EvA9%2Fbtrat2uQp1f%2FAAAAAAAAAAAAAAAAAAAAAA5pz1Gq3UNd_eBik8a6Hu_a_Vv9_UKSiMfMb5ChL2XC%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3D71YNPm%252F5khTY7%252FKHviYrPTrOZ84%253D)