일단 문제 설명에 앞서 너무 어려웠다. 어려워서 짜증이 치밀어 오르다가 여러 사람의 풀이를 참고해보고 스스로 풀기를 반복하여 겨우겨우 풀었다.

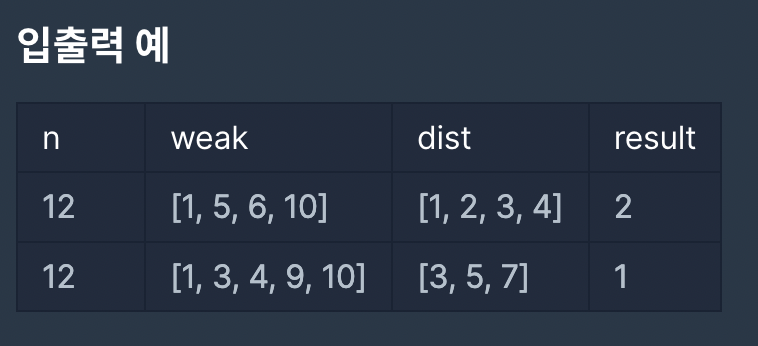
문제를 읽어보면 크게 별게 없다. 취약한 지점이 존재하고 최대한 적은 친구들을 사용하여 취약한 지점을 점검하고 오는 것이다. 이때 사용된 친구들 수의 최솟값을 구하면 된다. 그런데 문제는 어디에서 시작해야할지, 어떤 친구를 투입할지 여러가지 고민이 필요하다.
처음에는 그리디 냄새가 났다. 어떤 취약한 지점을 고르고 가장 이득이 큰 부분을 선택하는 방식으로 진행하려고 했지만 기준을 만드는게 어려웠고 어떻게 구현을 해야하나 고민되었다.
그런데 n은 200이하이고, weak배열은 15이하, dist배열도 8이하였다. 그렇다면 완전 탐색으로 모든 경우를 해볼수도 있겠다는 생각이 들었다.
처음에는 1,5,6,10으로 차례로 친구들을 투입할 수 있지만, 문제는 5,6,10으로 투입하게 된다면 마지막 1까지의 계산을 하는게 불편하다. 그래서 원형벽을 2배로 만들어 버린다. 그러면 5,6,10,13위치로 친구들을 차례로 투입할 수 있게 된다.
weak는 길이가 4인 배열이기 때문에 4번의 연산을 해보면 된다.
1. [ 1, 5, 6, 10]
2. [ 5, 6, 10, 13]
3. [ 6, 10, 13, 17]
4. [ 10, 13, 17, 18]
이제 1번 연산인 [ 1, 5, 6, 10 ]의 취약점을 도는 경우 어떻게 친구들을 투입해야할까? A친구를 투입했을때 친구가 갈수 있는 최댓값이 다음 탐색할 취약점까지 도달하는지 아닌지를 판단해야한다. A친구가 4거리를 갈수 있다 가정한다. 그럼 1에서 출발하여 4거리를 가기 때문에 5까지 도달가능하다. 그러면 5취약점은 이미 도달가능한 상태기 때문에 6취약점에 새로운 B친구를 투입시킨다. B친구가 어디까지 갈 수 있는지는 1+4(A의 거리)+3(B의거리) = 8까지 도달가능하다.
이러한 방식으로 친구들을 투입할때 어디까지 도달가능한지 판별하여 몇명의 친구가 투입되는지 구하고 친구 사용수의 최솟값을 갱신시켜준다.
그런데 A,B,C,D의 친구를 차례로 투입시킬때 순서가 중요하다. 예를 들어 4,3,2,1로 투입시켜도 되지만 4,2,1,3으로 투입시키는게 이득일 수도 있다. 따라서 A,B,C,D친구들의 투입 차례를 순열로 만들어준다. 이를 통해 출발 취약점에 따른 모든 친구들 투입 상황을 구할 수 있다.
그럼 이 문제에서의 주요 포인트는 아래와 같다.
1. 원형 배열을 2배의 배열로 만들어서 쉽게 만들기
2. 친구들 투입 순서를 순열로 구하기
이제 코드로 구현해본다.
from itertools import permutations
def solution(n, weak, dist):
INF = 1000000000
answer = INF
Map = list(weak)
for i in weak:
Map.append(i+n)
_dist = list(permutations(dist))
for si in range(len(weak)):
for pi in _dist:
dist=pi
count = 0
nextpoint = -1
for i in range(si, si+len(weak)): # 몇번수행하는가
# 조건
if nextpoint >= Map[i]:
continue
if count >= len(dist):
count = INF
break
nextpoint = Map[i] + dist[count]
count+=1
answer = min(answer,count)
if answer == INF:
return -1
return answer'알고리즘' 카테고리의 다른 글
| [python3] 백준 1339 풀이 ( 단어 수학, 그리디 ) (0) | 2022.03.08 |
|---|---|
| [python] 코테 대비 알고리즘 모듈 정리 (0) | 2022.03.06 |
| [python3] 백준 4195 (친구 네트워크, 유니온 파인드) (0) | 2022.02.26 |
| [python3] 백준 2470 풀이 ( 투포인터 ) (0) | 2022.02.25 |
| [python3] 프로그래머스 섬 연결하기 ( 그리디, MST, 크루스칼, 유니온 파인드) (0) | 2022.02.25 |
![[python3] 프로그래머스 외벽 점검 ( 2020 KAKAO BLIND RECRUITMENT, level3, 완전탐색, 순열 )](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fyh5FQ%2FbtruxkXIpZo%2FAAAAAAAAAAAAAAAAAAAAAEbUeVKJnHYoTP7chqtuEaKrz-kw-k310tXCocV6eTY2%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DGYrQYHCRIRiakoRyLk0%252BQWzJdrM%253D)