항상 combinations로만 조합을 구했는데 이제는 한번 정리를 해야할것 같아서 오랜만에 글을 쓴다.
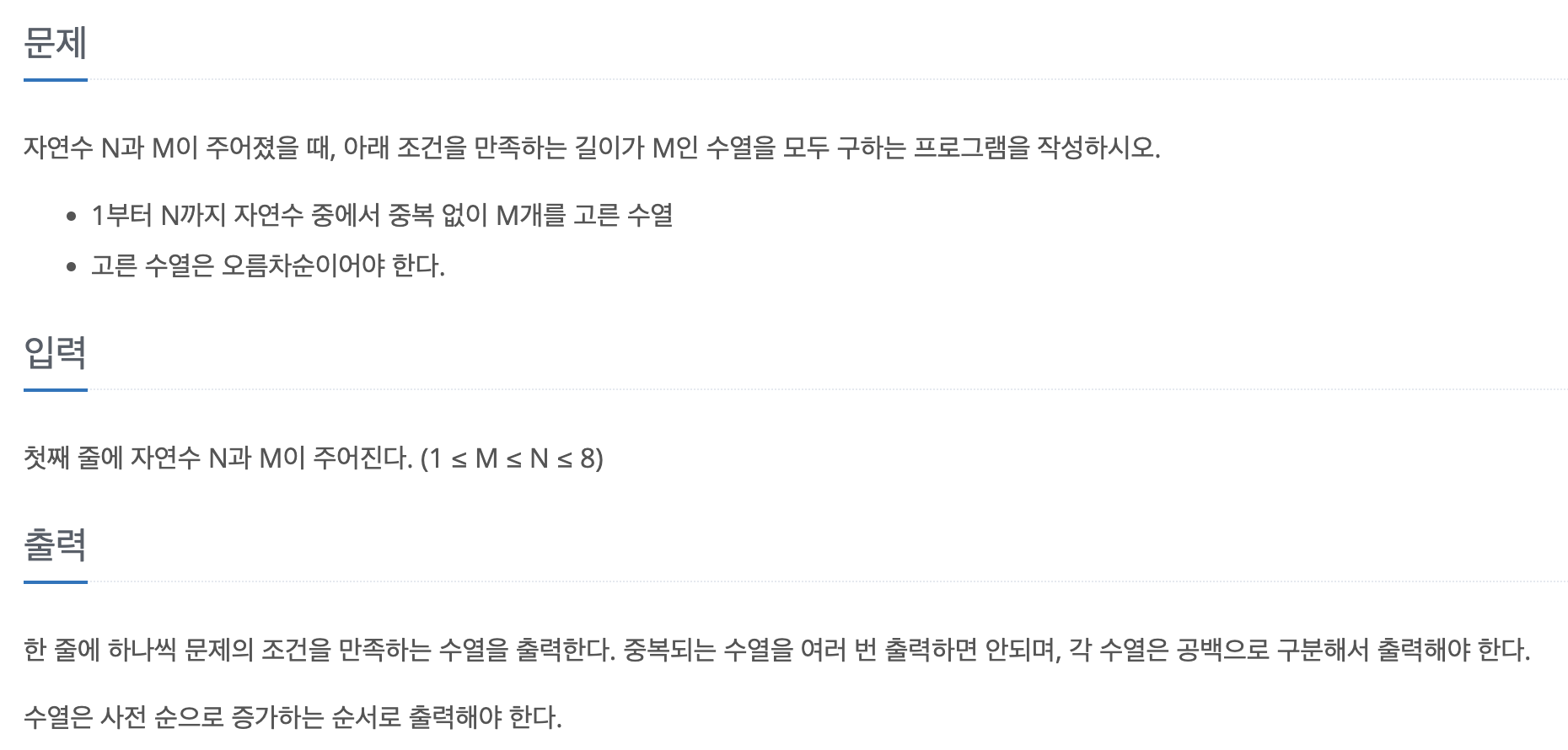
이문제는 백준 15650번으로 조합을 구하면 되는 문제이다. 사실 라이브러리를 사용한다면 상당히 쉬운 문제이다.
from itertools import combinations
N, M = map(int, input().split())
for com in list(combinations([i for i in range(1, N+1)], M)):
print(" ".join(map(str, com)))그러나 이렇게 푸는게 습관이 되어 나중에 백트래킹 문제가 어렵게 느껴졌고 기초적인 문제를 코테에서 틀리는 상황이 발생했다.
따라서 이걸 DFS로 풀어보자.
4에서 3개를 뽑는 경우는 [1,2,3],[1,2,4],[1,3,4],[2,3,4] 로 4가지 경우가 존재한다. 이것을 시각화하면 트리형태로 만들수 있다.

예를 들어 매번 노드가 존재하고 다음 노드가 적합한지 판단해야한다.예를 들어 1노드부터 시작하는경우
[1] 다음에 1이 들어올수 없다. 하지만 2,3,4는 들어올 수 있다. 일단 2를 넣는다.
[1,2] 다음에 1,2는 들어올 수 없다. 하지만 3,4는 들어올 수 있다. 일단 3을 넣는다.
[1,2,3]은 이미 구하고자 하는 3개를 뽑았다. 출력하고 되돌아간다.
[1,2] 다음에 1,2는 들어올 수 없다. 3도 이미 들어갔었다. 따라서 4를 넣는다.
[1,2,4]은 이미 구하고자 하는 3개를 뽑았다. 출력하고 되돌아간다.
:
:
이러한 방식으로 모든 노드를 매번 방문하는 것은 비효율적이므로 그 과정중에 불필요한 과정을 생략해줄 수 있다. 이것이 백트래킹이다. 따라서 이걸 코드로 나타내면 아래와 같다. 즉 탐색하면서 조건을 걸어 불필요한 과정을 쳐내는 형식으로 짜면 된다. 아래의 코드는 루프구문을 을 통해 불필요하게 방문했다고 판단하는 값을 돌지 않게 만들었다.
N, M = map(int, input().split())
tmp = [0] + [i for i in range(1, N+1)]
def DFS(i, L):
if len(L) == M:
print(" ".join(map(str, L)))
return
for j in range(i+1, len(tmp)):
DFS(j, L+[tmp[j]])
DFS(0, [])
이제 이걸 변형하면 permutations같은 순열을 만들수도 있고 다양한 조합과 순열을 만들수 있다.
'알고리즘' 카테고리의 다른 글
| [python3] 백준 1991 (트리 순회, 트리, 재귀) (0) | 2022.03.26 |
|---|---|
| [python3] 1167 풀이 (트리의 지름, 트리, DFS) (0) | 2022.03.25 |
| [python3] Trie 구현 (0) | 2022.03.19 |
| [dp] 모듈러 분배법칙 (0) | 2022.03.12 |
| [python3] 백준 1939 풀이 ( 중량제한, MST, 유니온 파인드 ) (0) | 2022.03.09 |
![[python] 조합을 DFS로 구하기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F14TbT%2FbtrxdOO1wtj%2FAAAAAAAAAAAAAAAAAAAAAK-iDeebUbEMArI32a4QXioyxXh9pbsUdGftK2Q1rSza%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DxmB7dIigvwDHoleuGfDDkun6IT8%253D)