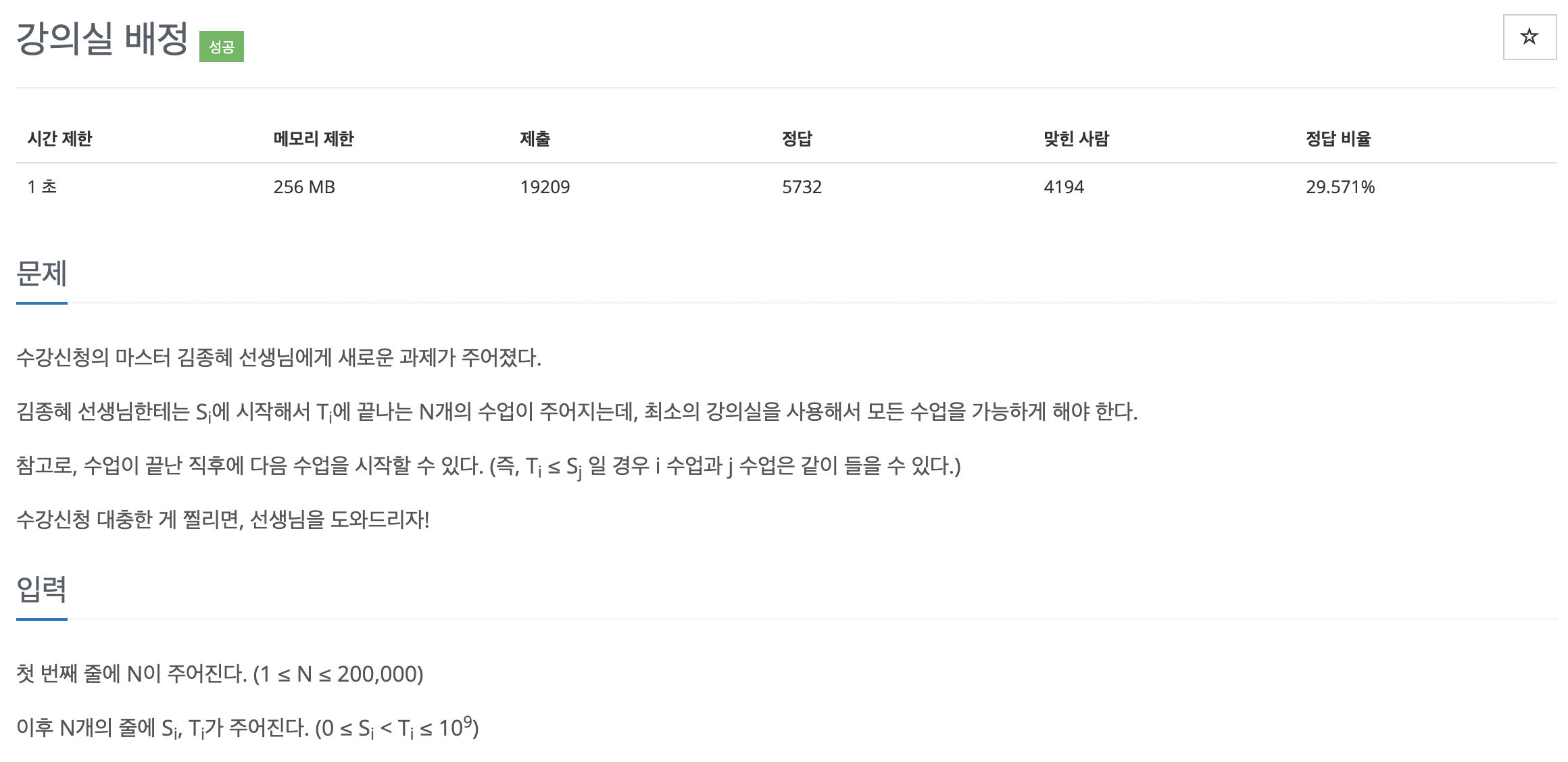
1~3시, 2~4시, 3~5시의 강의가 존재할때 최소 몇개의 강의실이 필요한지 구해야한다.
보통 강의실 문제는 그리디로 하나의 강의실이 존재할때 몇개의 수업이 가능한지는 물어보는 문제가 많았던거 같은데 이번에는 강의가 존재할때 몇개의 강의실이 필요한지 구해야한다.
처음에는 갈피를 못잡았다. 그리디 같은 느낌이 들어서 정렬을 해보고 구하려고 했는데 잘 구해지지 않았다. 그래서 알고리즘 분류를 보니 예상도 못한 우선순위 큐가 존재했다.
우선순위 큐를 사용해야한다는 힌트를 보자 바로 풀이가 떠올랐다.
우선 우선순위 큐에 들어가야하는것은 강의실이 될 수 있다. 즉, 해당 강의실을 몇시부터 몇시까지 쓰는 큐가 된다.
처음에는 1-3시에 강의실을 사용할 것이기 때문에 큐에 A(1-3)으로 넣는다.
2-4강의는 A(1-3)강의실을 사용할 수 없으므로 B(2-4)를 새롭게 넣는다. 그럼 큐는 A(1-3),B(2-4)가 된다.
3-5강의는 A(1-3)강의실을 그대로 사용가능하므로 A(1-3)을 A(1-5)로 바꾸어 넣는다. 그럼 큐는 B(2-4),A(1,5)가 된다.
그럼 최종적으로 필요한 강의실은 2개가 된다.
(이때 우선순위 큐는 강의가 제일 빨리 끝나는 우선순위로 동작하게 한다.)
이러한 방식으로 풀이를 진행하면 된다.
"""
알고리즘 분류 보고 풂
그리디 + 최소힙
강의시간이 존재할때 힙에 리스트형태로 강의실의 사용시간을 기재하여
가장 빨리 끝나는 강의실을 사용할 수 있도록 구현
"""
import heapq
import sys
input = sys.stdin.readline # N <= 200000 이므로 입력받는 숫자가 크기 때문에 선언
N = int(input())
hq = [] # 강의실을 저장할 hq
cl = [] # 강의시간을 받는 리스트
for n in range(N):
a, b = map(int, input().split())
cl.append([a, b])
cl.sort() # 모든 강의실을 받은 후에 가장 빨리 시작하는 순으로 정렬
for c in cl:
a, b = c # 강의의 시작시간 a, 강의의 종료시간 b
if len(hq) == 0:
heapq.heappush(hq, [b, a])
continue
# 강의실중 가장 끝나는 시간이 빠른경우를 뽑아온다. 이때 hq에 들어가는 인자는 [강의종료, 강의시작]
end, start = heapq.heappop(hq)
if end <= a:
heapq.heappush(hq, [b, start]) # 강의실을 사용할 수 있는 경우 시간을 누적하여 hq에 선언
else:
# 강의실을 사용할 수 없는 경우 기존에 pop한 강의실을 넣어 원상복구
heapq.heappush(hq, [end, start])
heapq.heappush(hq, [b, a]) # 강의실을 사용할 수 없기 때문에 새로운 강의실을 추가해준다.
print(len(hq))'알고리즘' 카테고리의 다른 글
| [python3] 백준 7579 (앱 , DP) (0) | 2022.05.27 |
|---|---|
| [python3] 백준 1039 (교환, BFS) (0) | 2022.05.22 |
| [python3] 백준 1991 (트리 순회, 트리, 재귀) (0) | 2022.03.26 |
| [python3] 1167 풀이 (트리의 지름, 트리, DFS) (0) | 2022.03.25 |
| [python] 조합을 DFS로 구하기 (0) | 2022.03.25 |
![[python3] 백준 11000 (강의실 배정, 최소힙, 그리디)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FH1MBB%2FbtrBA0imTwT%2FAAAAAAAAAAAAAAAAAAAAANnHyL0eJy1SMSl1n5xFk3sJO4WyUqNSOWcbW7LDOe7E%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3Dh2y9cSvQq66NxPtgJ281yvcnhgc%253D)