

접근
단어를 조합해서 비용을 최소로 만들어야 하는데 문제는 매번 다른 단어를 어떻게 조합할지가 문제다.
예를 들어 neotowheret 라는 단어가 존재할때 ne를 선택하면(문제에는 없지만 가능하다 가정하면) 비용이 0이지만, one을 선택한다면 비용이 3이다.
따라서 ne를 선택하는게 합리적으로 보이지만 ne이 이후에 가능한 단어의 조합이 없기 때문에 ne가 아닌 one을 선택해야한다.
즉, 어떤 단어를 선택해서 조합할지 + 단어를 선택하는 경우 최소비용을 적용하는등의 다양한 조합이 필요하다.
처음에는 각 단어가 가질 수 있는 모든 조합을 만들어서 대입하여 풀까도 생각했다. 예를들어 one이라면 noe,eno,oen,eon,neo 등등 모든 케이스를 뽑아서 적용하는 것이다. 그러나 50개의 단어에 대해서 모든 permutations를 구한다면 케이스가 너무 많기 때문에 불가능하다.
따라서 완탐을 해야하는데 완탐을 하는경우에 생각 해볼 수 있는게 DP다.
그래서 DP적으로 풀기위해서는 어떻게 해야할지 고민해볼 수 있었다.
풀이
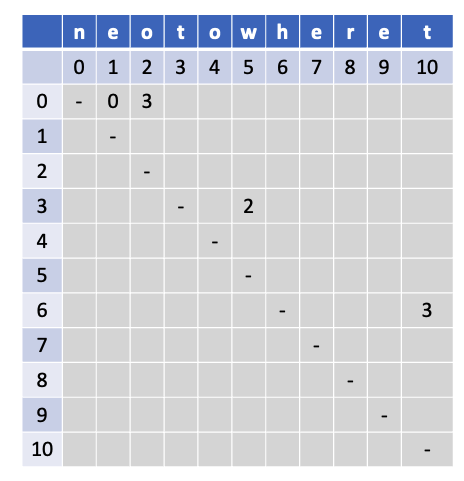
그러면 dp[0][1]은 0인덱스부터 1까지 가능한 최소비용을 나타낸다. 따라서 ne에 대해 ne를 대입하면 0이 나오고,
dp[0][2]은 0인덱스부터 2까지 가능한 최소비용을 나타내면 neo는 one과 3차이나므로 3이 된다.
dp[3]5]은 tow와 two는 2가 차이나므로 2가된다.
dp[6][10]는 heret과 three는 3차이나므로 3이 된다.
만들어본 그래프는 이해를 돕기위해 잠깐 표현한 것이고 이걸 1차원 배열로 줄일 수 있다.
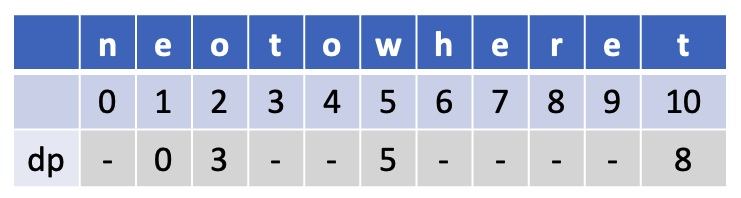
위와 같이 배열을 만들어 주는게 가능하다.
점화식을 표현하자면 dp[end] = min(dp[end], dp[start-1] + 최소비용(문장[start][end])) 가 된다.
이때 최소비용을 구하기 위해서는 매번 해당되는 문장[start][end]를 만족하는 단어를 찾고, 비용을 구하면된다.
이게 가능한 이유는 주어지는 문장이 50글자 밖에 안되기 때문에 최대 250번만 연산 하면 되기 때문이다.
(*처음알았는데 dic 비교연산자가 꿀이었다. 예를 들어 {1:2,2:3} 과 {2:3,1:2}를 비교하면 같은 해쉬함수를 써서그런지 True가 나온다. 이를 활용하여 빠르게 알파벳 구성을 비교할 수 있었다.)

구현
S = input()
N = int(input())
words = []
D = {}
for n in range(N):
word = input()
words.append(word)
D[word] = {}
for i in word:
if i in D[word]:
D[word][i] += 1
else:
D[word][i] = 1
words.sort(key=lambda x: len(x))
INF = 1000000
dp = [INF for i in range(len(S))] + [0]
for e in range(len(S)):
targetDic = {}
for s in range(e, -1, -1):
target = S[s:e+1]
if S[s] not in targetDic:
targetDic[S[s]] = 1
else:
targetDic[S[s]] += 1
for i in range(N):
word = words[i]
# 길이 검증
#if len(target) != len(word):
# continue
# 철자 검증
if D[word] != targetDic:
continue
# 몇이나 차이나는지
count = 0
for j in range(len(word)):
if target[j] != word[j]:
count += 1
dp[e] = min(dp[e], dp[s-1] + count)
if dp[len(S)-1] == INF:
print(-1)
else:
print(dp[len(S)-1])'알고리즘' 카테고리의 다른 글
| [python3] 백준 7579 (앱 , DP) (0) | 2022.05.27 |
|---|---|
| [python3] 백준 1039 (교환, BFS) (0) | 2022.05.22 |
| [python3] 백준 11000 (강의실 배정, 최소힙, 그리디) (0) | 2022.05.08 |
| [python3] 백준 1991 (트리 순회, 트리, 재귀) (0) | 2022.03.26 |
| [python3] 1167 풀이 (트리의 지름, 트리, DFS) (0) | 2022.03.25 |
![[python3] 백준 1099 (알 수 없는 문장, DP)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdegVSi%2FbtrENHhEUhc%2FGjOHI7FfC4KnEcj0L3EsVk%2Fimg.png)