이번 문제 너무 어려웠다. 이것저것 해보다가 결국 해설을 봐버렸지만 그냥 외워서 체득시켜 놓아야 겠다.
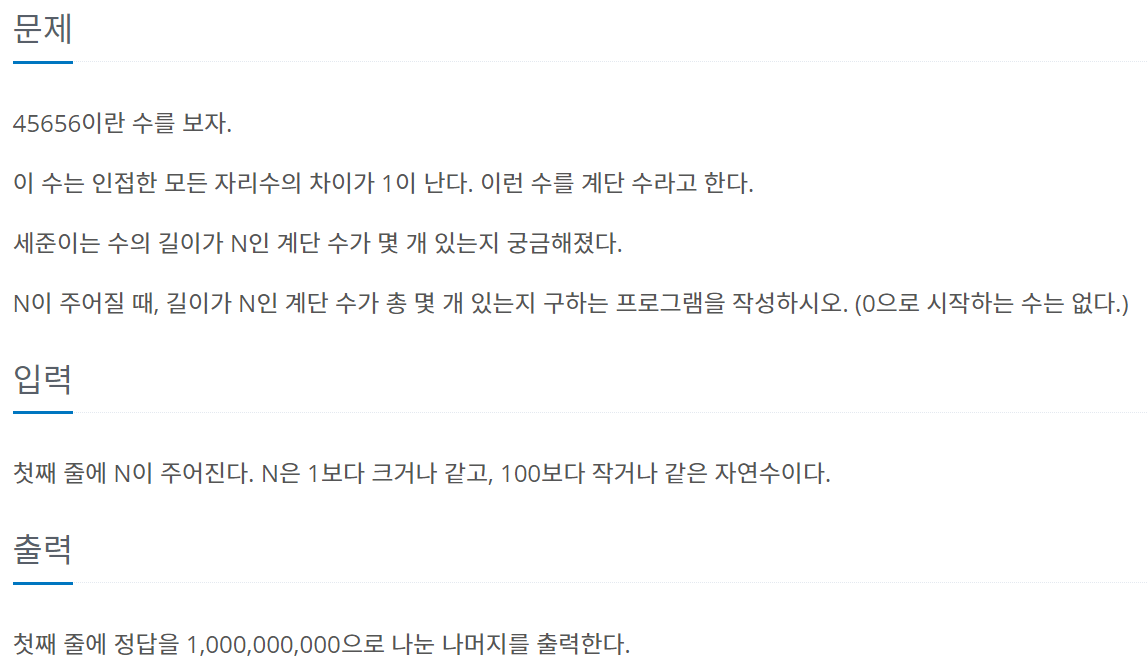
솔직히 이거 못풀었다. 그래서 해설을 보고 이해하고 풀게 되었다.
처음에는 노가다로 갯수를 구해보았다.
9, 17, 32, 61까지 구했고 먼가 규칙이 있는듯 했지만 결과만으로는 규칙을 찾을 수 없었다.
그래서 끝자리를 배열에 넣어 개수를 확인하는 방식을 사용해보았다. 그러나 이렇게 풀면 시간초과가 났다.
알고보니 배열을 2차원 배열을 만들어 각 숫자별 개수를 저장하여 푸는 방법이 존재했다.
예를 들어 끝자리가 가능한 숫자는 0~9까지 이다. 따라서 이에 대한 배열을 만든다.
그리고 N=1일때 가능한경우에 1을 채워준다. 0은 시작부분에 나올수 없기 때문에 0이 되고 나머지는 가능하므로 1을 채울 수 있다.
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
그러면 합은 9가 된다.
이번에는 N=2일때를 구해본다.
두번째 숫자가 0인경우는 이전에 1인 경우에 가능하므로 1을 그대로 받아준다.
두번째 숫자가 1인 경우에는 이전에 0인 경우와 2인 경우이다. 따라서 0과 1을 받아준다.
두번째 숫자가 2인 경우에는 이전에 1인 경우와 3이 경우이다. 따라서 1과 1일 받아준다.
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0+1 | 1+1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
그럼 대략 점화식을 구할 수 있다.
기본 점화식은 dp[i][j] = dp[i-1][j-1]+dp[i-1][j+1] 가 된다.
단 j가 0이거나 9라면 dp[i][j] = dp[i-1][j+1], dp[i][j] = dp[i-1][j-1] 로 구하면 된다.
따라서 이를 코드로 바꾸는 것은 쉽다.
n=int(input())
dp =[[0 for i in range(10)] for i in range(101)]
for i in range(1,10):
dp[0][i] = 1
for i in range(1, n):
for j in range(10):
if j ==0:
dp[i][j] += dp[i-1][j+1]
continue
if j == 9:
dp[i][j] += dp[i-1][j-1]
continue
dp[i][j] += dp[i-1][j-1] + dp[i-1][j+1]
print(sum(dp[n-1])%1000000000)결과적으로 문제를 해결할 수 있었다. 그러나 답안을 보고 푼 문제라 아쉬움이 많았다.
다음에는 DP를 풀때 1차원이 안된다면 2차원을 어떻게 사용할 수 있을지 고민해보는 습관을 들여야 할 것 같다.
'알고리즘' 카테고리의 다른 글
| [python3] 백준 2252 풀이 ( 줄세우기, 위상정렬, DAG, 그래프 ) (0) | 2021.08.07 |
|---|---|
| [c++] 백준 11657 풀이 ( 타임머신, 최단경로, 벨만-포드, 음수 가중치 ) (0) | 2021.08.06 |
| [c++] 백준 1753 풀이 ( 최단 경로, 다익스트라, 그래프, 우선순위 ) (0) | 2021.08.04 |
| [c++] 백준 1197 풀이 (MST, 최소 신장 트리, 그래프, 유니온 파인드) (0) | 2021.08.02 |
| [c++] 백준 1717 풀이 (집합의 표현, 그래프, 서로소 집합, 유니온파인드) (0) | 2021.07.26 |
![[python3] 백준 10844 풀이 ( 쉬운 계단 수, 다이나믹 프로그래밍, 이차 배열)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FWfsWG%2Fbtrbe40iket%2FAAAAAAAAAAAAAAAAAAAAAJY1R6nqlV21HxzCAxsVbttSyX9Ub5TWKtDAqpnmzpie%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DS%252BS%252BuIpwvUpQcUSMQOvUN4y14TA%253D)