[python3] 백준 2252 풀이 ( 줄세우기, 위상정렬, DAG, 그래프 )

위상정렬

어떤 일을 하는 순서를 찾는 알고리즘, 즉 순서가 정해져 있는 일을 차례대로 수행하는 것이다.

1. 답이 여러개 가능
2. DAG(Directed Acyclic Graph)에만 적용 가능
3. 큐나 스택을 사용

DAG(Directed Acyclic Graph)

방향성 비순환 그래프는 개별요소들이 특정한 방향을 향하고, 순환하지 않는것. ( o -> o -> o 요런 형태)

사실 그냥 봐서는 잘 이해가 가기 어렵다. 그러므로 고수님의 링크(https://gmlwjd9405.github.io/2018/08/27/algorithm-topological-sort.html)

대강 어떤 알고리즘인지 알았다면 문제를 보자

문제를 쓰윽 보면 키 순서대로 학생을 정렬하려고 하는데 모든 학생의 비교 결과가 아닌 일부의 비교 결과만 제공한다.
따라서 일부의 비교 결과를 통해 학생들을 줄세우면 된다.
우선, 키를 비교하기 때문에 크고 작음으로 비교를 하게 되면 그래프는 DAG그래프의 형태를 띄게 된다. 또한 위상정렬의 특징중 하나인 답이 여러가지인 경우에는 아무거나 출력하라고 한다. 따라서 위상정렬을 이용하여 줄을 세우면 되겠다는 생각이 든다.

예시 2번인 경우를 그래프로 나타내 보면 DAG형태를 띈다.  4->2 3->1

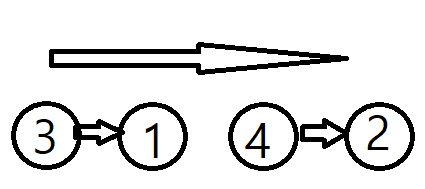
그럼 위상 정렬의 원리가 어떻게 되는지 이해해봐야한다. 전략은 이러하다.

1. 각 노드별로 진입차수를 설정해준다.(A->B인경우 B의 진입차수는 1, A->B, C->B의 경우 B의 진입차수는 2)
2. 진입차수가 0인 노드(즉, 각 그래프의 루트격의 노드들)들을 큐에 삽입한다.
3. 진입차수를 낮추기 위한 루프를 진행한다.
4. 큐에서 노드를 뽑고 최종 큐에 삽입한다.
5. 큐에서 뽑았던 노드와 접점하는 노드를 찾아서 진입차수를 1낮춰준다.
6. 만약 진입차수가 0이라면 큐에 삽입한다.
7. 최종 큐의 갯수가 노드들의 개수와 동일하면 루프를 종료한다.(모든 노드의 정렬이 최종큐에서 완료된 것이기 때문)

자, 아마도 이렇게 글만 주르륵 보면 절대 이해가 안갈 것이다. 이해하면 천재다.
예시를 토대로 그림으로 나타내 보자.

4 2
4 2
3 1

위의 예제가 주어진다면 그래프는 아래와 같고, 진입차수 배열과 q가 필요하다.

3,4노드의 진입차수가 0이므로 큐에 3,4를 넣는다.

q에서 3을 뽑고 3과 연결된 1의 진입차수 1개를 줄인다. 그럼 1의 진입차수가 0이므로 큐에 1을 넣는다.

이제 q에서 4를 뽑고 4와 연결된 2의 진입차수를 1줄인다. 그럼 2의 진입차수는 0이므로 큐에 2를 넣는다.

이제 q에서 1을 뽑고 1과 접점을 구한다. 그런데 없다. 그러므로 더 이상 연산을 진행하지 않는다

이제 q에서 2를 뽑고 접점을 확인한다. 그러나 점점이 없으므로 연산을 진행하지 않는다.

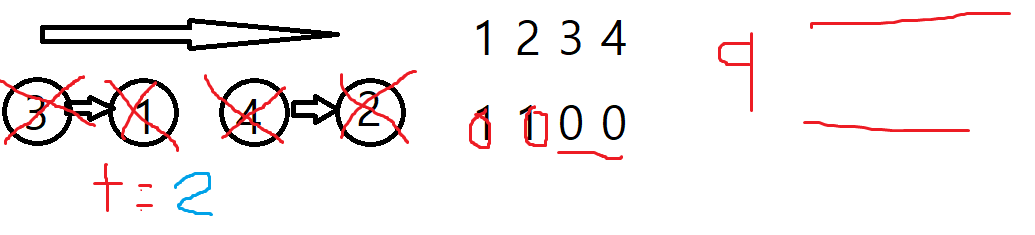
그럼 결과적으로 t가 뽑힌 순서인 3,4,1,2가 위상정렬의 결과이다. 혹시 이 허접한 그림을 봐도 이해가 되었다면 당신은 정말 똑똑한 것이다. 그럼 어떤 원리로 동작하는지 그림으로도 살펴 봤으니 이제 실제 코드를 보면서 이해한다면 더 이해가 쉽다.

# 위상정렬 = 어떤 일을 하는 순서를 찾는 알고리즘
# 인접배열, 위상정렬용 배열, 탐색용 q배열, 최종 total배열 사용
from collections import deque
n,m = map(int, input().split())
graph = [[]for i in range(n+1)]
numMap = [0 for i in range(n+1)]

for i in range(m):
    a,b = map(int, input().split())
    graph[b].append(a)
    graph[a].append(b)
    numMap[b] += 1

q = deque([])
# q에 탐색할 노드를 넣어준다.
for i in range(1,n+1):
    if numMap[i] == 0:
        q.append(i)

total = []
while q:
    t = q.popleft()
    total.append(t)
    childs = graph[t]
    for child in childs:
        if numMap[child] == 0:
            continue
        else:
            numMap[child] -= 1
            if numMap[child] == 0:
                q.append(child)
for i in total:
    print(i, end=' ')

코드로 짜는 것은 어렵지 않다. 다만 이러한 알고리즘을 생각하는게 어려운거 같다. 

 

결론 : 위상정렬은 방향성 비순환 그래프(DAG)일 때 사용가능하며 답이 여러개이다. 아직 어제 정확하게 위상정렬을 사용해야 하는지는 잘 모르겠다. 관련 예제를 더 풀어보아야겠다.