이 문제는 예전에 파이썬으로 풀었던 적이 있다. 그러나 c++풀이는 또 다른 포인트가 있기때문에 다시 풀어보기로 했다.
일단 문제를 쓱 보자
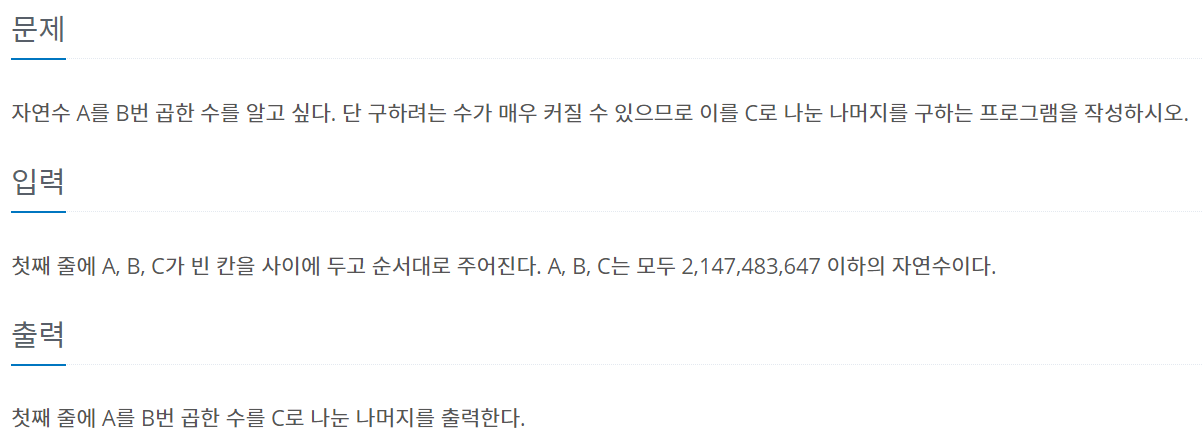
문제를 보면 A를 B승하고 C로 나눈 나머지를 구하라는 뜻이다.
A,B,C 모두 21억을 넘는다. 이는 int의 최댓값 범위이다. 그렇다면 A^2일때 int를 넘어가서 오버플로우가 난다. 따라서 int보다는 long long을 사용하여 함수를 작성하는게 좋을 것 같다.
long long의 범위는 9,223,372,036,854,775,807 이다. 그런데 A는 21억이기 때문에 long long범위를 초과할 가능성도 있다고 생각했다. 21억에 붙은 0은 9개, long long 범위의 0개수는 18개이다. 즉, 연산중에 long long범위를 초과할 가능성이 존재하는 것이다. 따라서 중간중간 c로 나누어주어야 한다.
만약 B의 개수만큼 연산을 진행한다고 가정한다면 int범위인 21억번 계산을 해야한다. 따라서 분할정복을 이용하여 계산 횟수를 줄일 수 있다.
예를 들어 10^11이라면 10을 11번 곱해야한다.
그러나 연산의 값을 반 씩 나누어 구한다면 계산 횟수를 log11로 줄일 수 있다.(명확하게 맞는지는 잘 모르겠다. 그런데 시간이 확실히 줄어든다.)
따라서 10^11을 구하기 전에 10^5를 구하고 10^5를 구하기 전에 10^2를 구하고 10^2를 구하기 전에 10^1을 구해서 필요한 곳에 사용만 해주면된다. 이에 대한 설명은 다른 곳에도 잘 나와있고 어렵지 않으니 넘어간다.
그럼 포인트는 아래와 같다.
1. 분할정복을 이용해 연산을 진행한다.
2. 오버플로우를 막기 위해 %c 를 중간마다 실행한다.
이를 토대로 코드를 작성한다. (pow함수를 사용하면 안된다. 왜냐하면 pow의 반환값이 int이므로 A*A를 하면 오버플로우가 일어나서 잘못된 값을 반환한다.)
#include<iostream>
using namespace std;
long long A, B, C;
long long divide(long long a, long long b, long long c) {
if (b == 1) { // 탈출조건
return a % c;
}
long long tmp = divide(a, b/2, c) % c;
if( b % 2 == 0 ){//짝수면 구한거 바로 더하기
return tmp * tmp % c;
}
else {//홀수면 나누고 a한번 더 곱
return tmp * tmp % c * a % c;
}
}
int main() {
cin >> A >> B >> C;
cout << divide(A, B, C);
}
'알고리즘' 카테고리의 다른 글
| [python3] 백준 2293 풀이 ( 동전 1, 다이나믹 프로그래밍 ) (0) | 2021.08.10 |
|---|---|
| [python3] 백준 9465 풀이 ( 스티커, 다이나믹 프로그래밍, 이차원 배열 ) (0) | 2021.08.09 |
| [python3] 백준 2252 풀이 ( 줄세우기, 위상정렬, DAG, 그래프 ) (0) | 2021.08.07 |
| [c++] 백준 11657 풀이 ( 타임머신, 최단경로, 벨만-포드, 음수 가중치 ) (0) | 2021.08.06 |
| [python3] 백준 10844 풀이 ( 쉬운 계단 수, 다이나믹 프로그래밍, 이차 배열) (0) | 2021.08.05 |
![[c++] 백준 1629 풀이 ( 곱셈, 분할 정복을 이용한 거듭제곱, long long )](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FEnCsd%2FbtrbyH3SvzT%2FAAAAAAAAAAAAAAAAAAAAAKHvbhqEhhFgvhsSW2GyIiVpntKK7wyMdGreuT8r3v6q%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DLIOYkVhfrV5pdDKDuTIasukUZOs%253D)